• 19. ANOVA summary

Links to: Summary. Chatbot tutor. Questions. Glossary. R packages. R functions. More resources.

Chapter summary

Enjoy this “insomnia meme” about the ANOVA. From this video

We previously introduced F and the ANOVA approach as an alternative to the two sample t-test. Here we show it’s true utility - by testing the single null hypothesis that all sample come from the same statistical population, we avoid the “multiple testing problem.” As such, compared to the naive testing of all pairwise differences, the ANOVA approach allows us to farily test for differences in means among numerous groups. If we reject the null that all groups are equal, we conduct a “post-hoc” test to see which groups differ.

Chatbot tutor

Please interact with this custom chatbot (ChatGPT link here, Now Gemini alllows us to share gems! Gemini link here). I have made to help you with this chapter. I suggest interacting with at least ten back-and-forths to ramp up and then stopping when you feel like you got what you needed from it.

Practice Questions

Try these questions! By using the R environment you can work without leaving this “book”. I even pre-loaded all the packages you need!

Setup

Fiddler males have a greatly enlarged “major” claw, which is used to attract females and to defend a burrow. Darnell and Munguia (2011) suggested that this appendage might also acts as a heat sink, keeping males cooler while out of the burrow on hot days. To test this, they placed four groups of crabs into separate plastic cups and supplied a source of radiant heat (60-watt light bulb) from above. The four groups were intact male crabs; male crabs with the major claw removed; male crabs with the other (minor) claw removed (control), and intact female fiddler crabs. They measured body temperature of crabs every 10 minutes for 1.5 hours. These measurements were used to calculate a rate of heat gain for every individual crab in degrees C/log minute.

Rates of heat gain for all crabs are loaded here as crabs but can be downloaded from this link: https://raw.githubusercontent.com/ybrandvain/datasets/refs/heads/master/crabs.csv

Q1.a) There are four groups. How many potential pairwise comparisons are there? .

For 4 groups, the number of unique pairs is: \[\frac{k(k - 1)}{2} = \frac{4(3)}{2} = 6\]

Q1.b) What is the probability of incorrectly rejecting one true null (at the \(\alpha\) threshold of 0.05) if all of these nulls were true?

The probability of not incorrectly rejecting a true null is 0.95. To not falsely reejct any try nulls we need six such successes. \[0.95^6 \approx 0.735\] So the probability of incorrectly rejecting at least one true null is:

\[1 - 0.735 = 0.265 \]

---

Q2) Consider the plot above. Before running an ANOVA or posthoc test, which comparisons do you think is most lilely to be significantly different?

female x male major removed female x male minor removed intact x male major removed intact x male minor removed male major removed x male minor removed

---

Calculate the sample size, mean, and variance for each treatment

Q3) Compare the variance with in each treatment. What is the greatest fold difference in variance between treatments?

It's exactly the same Less than two-fold Between two and five-fold Between five and ten-fold More than ten-fold

Q4) With this difference in variance among groups, the assumption of homoscedasticity is

Probably not a major concern Somewhat worrisome, but we can plow ahead anyways A big concern, we must transform or try a Welch's ANOVA

---

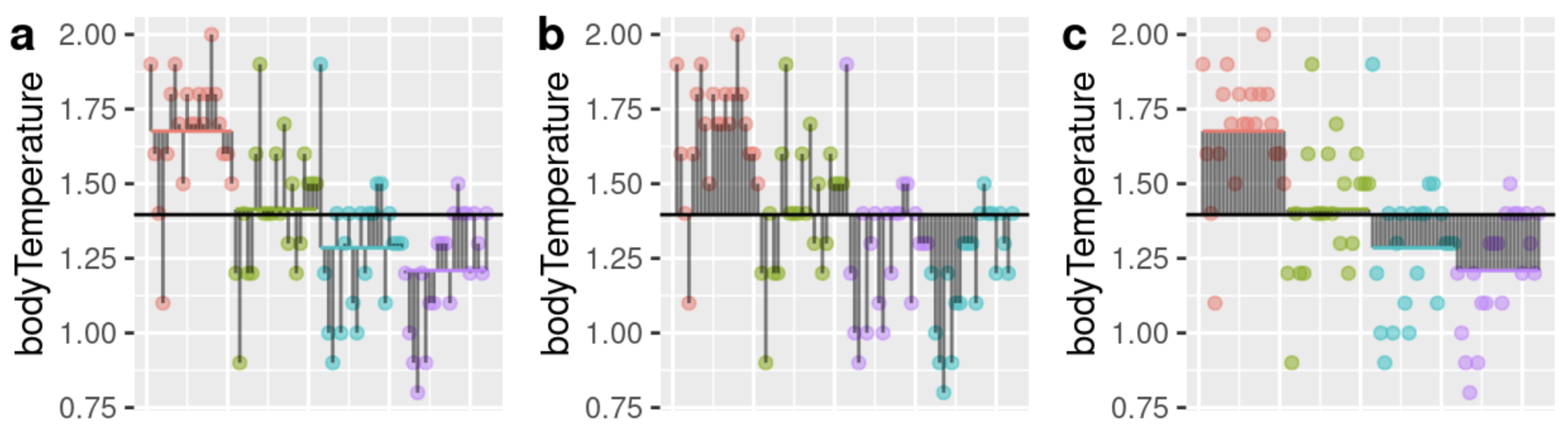
Q5.a) Which of the plots above shows total deviations? abc.
Q5.b) Which of the plots above shows model deviations? abc.
Q5.c) Which of the plots above shows error deviations? abc.

---

Assume we where using the code below to build an ANOVA for the crabs data

crabs                                          |>
    mutate(grand_mean = mean(bodyTemperature)) |>
    group_by(crabType)                         |>
    mutate(group_mean = mean(bodyTemperature)) |>
    ungroup()                                  |>
    summarise(this_partition = sum((group_mean - grand_mean)^2))

Q6) What would be the best name for this_partition? MS_totalMS_modelMS_errorSS_totalSS_modelSS_error

---

Q7.a) Why didn’t the code above work?

We did not load the broom pacakge We never generated augmented_crab you must use the original tibble, not augment() output to make a plot geom_qq expects the aesthetic to be called sample, not x

Q7.b) Fixing this error, which assumption are these plots meant evaluate?

Equal variance among groups Normal distirbutions of residuals Independence Unbiased data

Q7.c) Which wo of the plots are reasonable ways to evaluate this assumption. Fixing this error, which assumption are these plots meant evaluate?

Plot 1 and Plot 2 Plot 1 and Plot 3 Plot 1 and Plot 4 Plot 2 and Plot 3 Plot 2 and Plot 4 Plot 3 and Plot 4

---

Q8) In the context of an ANOVA, which R command gives you:

Q8.a) Estimates of model coefficients ONLY?

lm(y ~ x) |> anova() OR aov(y ~ x) |> summary() aov(y ~ x) |> TukeyHSD() lm(y ~ x)|> summary() lm(y ~ x)

Q8.b) An ANOVA table

lm(y ~ x) |> anova() OR aov(y ~ x) |> summary() aov(y ~ x) |> TukeyHSD() lm(y ~ x)|> summary() lm(y ~ x)

Q8.c) Results of post-hoc tests

lm(y ~ x) |> anova() OR aov(y ~ x) |> summary() aov(y ~ x) |> TukeyHSD() lm(y ~ x)|> summary() lm(y ~ x)

Q8.d) Model coefficients and standard errors, plus numerous potentially misleading p-values and t-values that should largely be ignored

lm(y ~ x) |> anova() OR aov(y ~ x) |> summary() aov(y ~ x) |> TukeyHSD() lm(y ~ x)|> summary() lm(y ~ x)

---

Run the relevant statistical tests below

---

Q9) Run an anova on the data. What do we do to the null hypothesis? Reject itFail to reject itAccept itFail to accept it

Q10) According to. the post-hoc test, if female intact is in significance group, “a”, which group(s) is intact male male major in? a onlyb onlyc onlya,ba,cb,ca,b,bc