• 19. Multiple testing problem

Motivating Scenario: You have sample with data from more than two groups. You wish to know if groups means differ from one another. This section explains why you cannot simply conduct all possible pairwise t-tests, and why you should instead use an ANOVA framework.

Learning Goals: By the end of this subchapter, you should be able to:

  1. Explain how conducting multiple tests inflates the overall (experiment-wise) false positive rate.

  2. Describe how ANOVA addresses the multiple testing problem by reframing it as a single hypothesis test.

  3. Know that there are alternative approaches to solve the multiple testing problem.

Six panels show pairwise comparisons of mean petal area among four Clarkia populations (SR, S22, S6, SM). Each panel contains two colored violins with overlaid points and black 95% confidence intervals. Some pairs appear different, others overlap, but all share the same vertical scale (0–0.7 cm²).
Figure 1: All six pairwise comparisons of mean petal area among four Clarkia xantiana parviflora hybrid zone populations. This presentation implicitly sets up six separate null hypotheses to test. Compare this to the figure in the first section, which showed data from all four sites together in one plot.

Multiple tests make a liar of your p-value

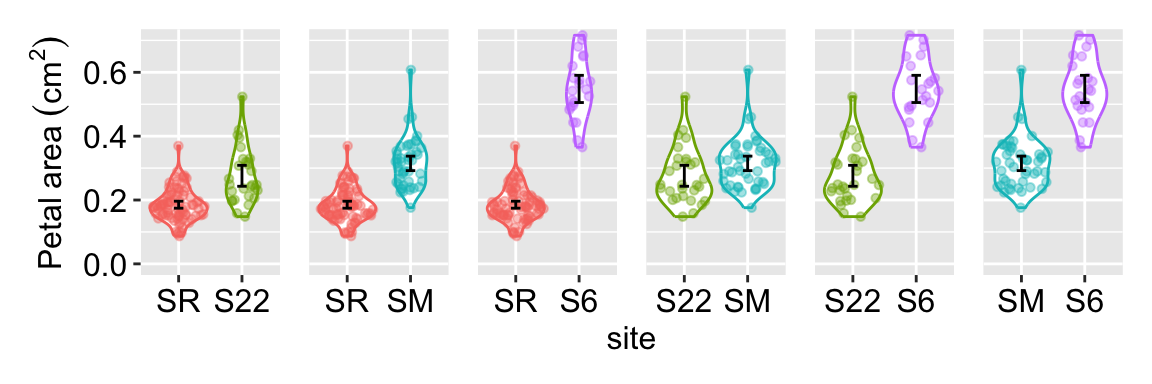
There are \({4 \choose 2} = 6\) possible pairwise comparisons of mean petal areas among the four Clarkia xantiana parviflora hybrid zone populations we studied (Figure 1). Even when all six nulls are true, there’s roughly a one in four chance that at least one test will falsely appear ‘significant.’ That’s because the probability all six avoid a false positive is \(0.95^6 = 0.735\).

Thus for this study our overall \(\alpha\) would be 1- 0.735 = 0.265, a value much larger than the \(\alpha = 0.05\) that was advertised. This problem gets pretty bad pretty quick (Figure 2). As such, conducting many t-tests on the same data makes your p-values misleading—they no longer represent the 5% false-positive rate we usually assume. When you run multiple tests, the chance of seeing at least one ‘significant’ result just by luck is much higher, so the reported p-values give a false sense of confidence

More broadly, the number of pairwise comparisons between n groups equals
\(n_\text{pairs} = \binom{n}{2} = \frac{n (n-1)}{2}\), and the experiment-wise false positive rate equals, \(1-(1-\alpha)^{n_\text{pairs}}\).

comparisons <- tibble(n_groups= 2:15)|>
    mutate(n_comparisons = choose(n_groups,2),
           experiment_alpha = 1-.95^n_comparisons)

ggplot(comparisons, aes(x = n_groups,  y =experiment_alpha))+
    geom_point(size= 4)+
    geom_line(linetype = 3, linewidth = 1.4)+
    labs(x = "# groups",
         y = "P(≥ 1 false positive)", 
         title ="The multiple testing problem")+
    theme(axis.text = element_text(size = 23),
          title = element_text(size = 23),
          axis.title = element_text(size = 23))+
    scale_x_continuous(breaks = seq(2,14,2))
The relationship between the number of groups (x-axis) and the probability of at least one false positive (y-axis). The curve begins near 0 when there are only two groups and rises steeply as the number of groups increases, illustrating how the overall false positive rate inflates as more pairwise tests are performed.
Figure 2: The probability of rejecting at least one true null hypothesis at the nominal α = 0.05 level when conducting all pairwise comparisons. With ten groups we have 45 pairwise comparisons and true experiment-wide α = 0.90.

ANOVA can solve the multiple testing problem

For p-values to be worth anything, they should correspond to the problem we set up. There are numerous ways to address the multiple testing problem (see below, and Wikipedia).

Instead of testing each combination of groups separately, ANOVA poses and tests a single null hypothesis — that all samples come from the same statistical population. This results in a well-calibrated null model (i.e. we will reject a true null with proability \(\alpha\)).

ANOVA hypotheses

  • \(H_0\): All samples come from the same (statistical) population. Practically, this says that all groups have the same mean.
  • \(H_A\): Not all samples come from the same (statistical) population. Practically this says that not all groups have the same mean.

But how do we see which groups differ? Our scientific hypotheses and interpretations depend not just on the single null hypothesis – “all groups are equal”– but on knowing which groups differ from one another. Later in this chapter we will introduce “post-hoc tests”, which - in combination with an ANOVA test which pairs of groups differ from one another.

That is, ANOVA shows whether groups differ; post-hoc tests show which groups differ.

xkcd’s classic description of the multiple testing problem (and the related communication and hype cycle). The original rollover text said: ‘So, uh, we did the green study again and got no link. It was probably a–’ ‘RESEARCH CONFLICTED ON GREEN JELLY BEAN/ACNE LINK; MORE STUDY RECOMMENDED!’ For more discussion see the associated explain xkcd.

Other ways to handle multiple comparisons

ANOVA solves the multiple-testing problem by asking one big question instead of many small ones. But sometimes we really do need to test many hypotheses e.g., when comparing every pair of groups, analyzing many traits, or in genome wide association studies etc. So there are other approaches to deal with this issue.

The Bonferroni correction is the simplest correction for multiple tests. A Bonferroni correction creates a new \(\alpha\) threshold by dividing your stated \(\alpha\) by the number of tests. So, if you test five different nulls at an \(\alpha = 0.05\), you apply the the Bonferroni by only rejecting the null when \(p<0.01\).

As the number of comparisons increases this correction becomes overly conservative, so people turn to other methods.

The False Discovery Rate (FDR) Rather than considering any false positive, FDR based methods consider the expected proportion of false positives among the results we call significant. So FDR based corrections ensures that on average, about 5% of the results we call ‘significant’ are actually false positives.