| lower_ci | upper_ci |
|---|---|
| 0.1054 | 0.2066 |
| 0.1092 | 0.1922 |
| 0.1090 | 0.2001 |
| 0.1152 | 0.1947 |
| 0.1092 | 0.1982 |
• 12. Gotchas
Motivating Scenario: We are amazed by our newfound power of estimating uncertainty by bootstrapping! But before we get carried away, we wonder if there’s anything we need to consider”
Learning Goals: By the end of this subsection, you should be able to:
- Know when to be wary of bootstrap-based estimates of uncertainty
- Consider the stability of bootstrap estimates of uncertainty, and the number of bootstrap replicates.
- Consider the size of the sample.
- Consider bias and non-independence of the sample.
- Know that there are other (common) ways to estimate uncertainty
Bootstrap gone wrong
Bootstrapping is great! It allows us to estimate uncertainty without relying on formulas or too many assumptions. But as with all stats tools, there are limits to the use of bootstrapping. So before moving onto the next section it is worth going over these limits and how to deal with them.
Bootstrapping itself is a sample
Bootstrapping uses sampling to approximate the sampling distribution. This means that every time we bootstrap we will get a different estimate of uncertainty - even if we have the same data going into the bootstrap. As with other forms of sampling, the more bootstrap replicates you make, the more stable your estimate of uncertainty is. However there is a trade-off between computational effort and the precision of bootstrap estimates of uncertainty.
How many bootstrap replicates are enough? I don’t know, and it depends on your data. I usually start with 1000 bootstrap replicates and calculate the bootstrap standard error and confidence intervals. I repeat this a few times and see if my estimates are stable.
If my estimated uncertainty bounces around a lot I increase the number of replicates to five thousand and see if that helps. I keep increasing the number of replicates until my estimates of uncertainty are stable.
If my estimate is stable I’m happy.
If the bootstrapping is taking forever, I decrease the number of reps.
Why not make millions of bootstrap replicates? It will take a lot of time, and overtax your computer with very little reward.
100 Bootstrap replicates: For me in this example, 100 bootstrap replicates leads to confidence intervals which are too variable to feel comfortable reporting.
5000 Bootstrap replicates By contrast estimates from 5000 bootstraps seem stable enough for me (e.g. I would declare that the lower CI is 0.107 and all that close enough).
| lower_ci | upper_ci |
|---|---|
| 0.1078 | 0.1983 |
| 0.1071 | 0.1992 |
| 0.1054 | 0.1978 |
| 0.1061 | 0.1991 |
| 0.1067 | 0.1984 |
Bootstrapping is unreliable when n is small
Bootstraping works by approximating the sampling distribution by resampling your data with replacement. Thus it inherently assumes your sample is a good representation of the population. A very small sample is unlikely to capture the true shape of the population’s distribution.
To think about this, consider an extremely small sample of two. Here bootstrapping will provide three estimates:
A quarter of the time we will sample individual one twice and their value will be the estimate of the mean.
Half the time we will sample both individuals so the mean of these two will be our estimate of the mean.
A quarter of the time we will sample individual two twice and their value will be the estimate of the mean. None of these are good estimates.
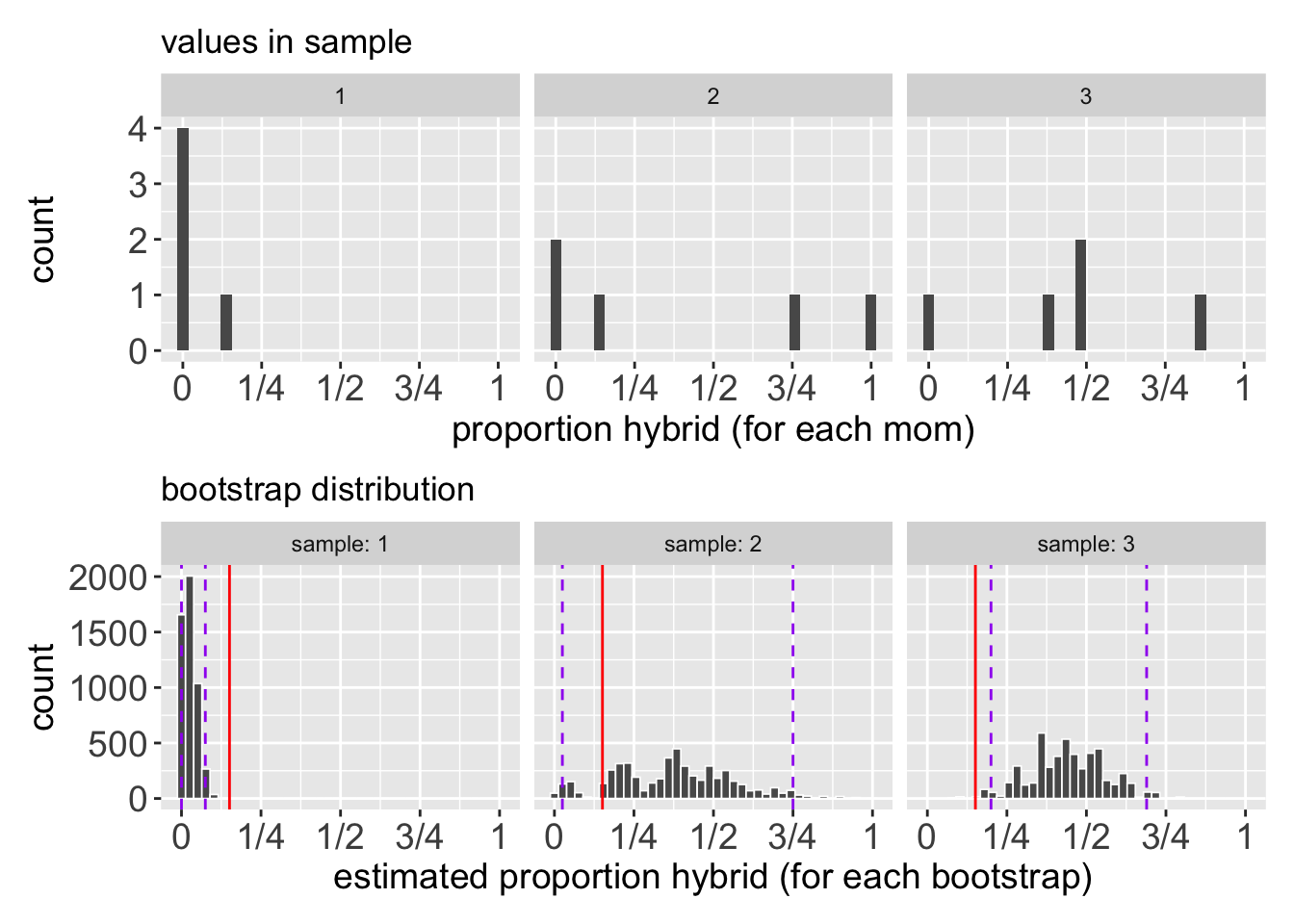
The bootstrap distribution is similarly limited for somewhat larger sample sizes. For example, Figure 2 shows the data and associated bootstrap distributions for three different samples of size five. The first consists of moms making zero or few hybrid seeds, the second has a mix of moms with few and many hybrid seeds, and the third consists of moms with many hybrid seeds. For the first and third samples, the 95% CI (purple dashed line in Figure 2) fails to capture the actual estimated mean from our original sample (red line in Figure 2).
As a rule of thumb, a sample of twenty or more is required for a reliable bootstrap estimate of uncertainty. But there is wiggle room and nuance - when data are less variable and more bell shaped we can get away with a smaller sample, while more variable data with strange distributions require a larger sample size for reliable bootstrapping.
Bootstrapping cannot fix bad sampling
More generally, resampling a poor sample will only give you a precise but wrong answer.
If data are non-independent, a simple bootstrap will not properly estimate uncertainty. Say we happened to sample intensely in a few sections of GC rather than sampling randomly across space. Within each section plants are likely to be more closely related genetically or to experience similar environmental influences etc which will make them more similar to one another. As such, our sample will not represent the variability of this population appropriately and we will be overconfident in our estimates.
If a sample is biased, a simple bootstrap will not properly estimate uncertainty. For instance, if you tended to sample more pink than white flowers because they were easier to see, the bootstrap would give you a precise estimate of a sample tilted toward more pink flowers than we see in the population. This will inflate our estimated probability of hybridization.
There are other ways to estimate uncertainty
Perhaps it’s my fault. I just love bootstrapping so much. But students sometimes finish this section thinking bootstrapping is the only way to estimate uncertainty. This is not true. While bootstrapping is very handy there are other – and more common approaches – to estimate uncertainty. These alternative approaches use common mathematical distributions to generate a sampling distribution and are therefore less computationally intense. We will encounter these later in the book.
