β€’ 11. Sampling summary

A stick figure holding an arm out towards an unseen crowd, is standing on a podium with five large bags around him, each having a dollar sign on it. Text bubble1: "Never stop buying lottery tickets, no matter what anyone tells you." Text bubble2: "I failed again and again, but I never gave up. I took extra jobs and poured the money into tickets.", Text bubble3: "And here I am, proof that if you put in the time, it pays off!" Caption below the panel: "Every inspirational speech by someone successful should have to start with a disclaimer about survivorship bias."
Figure 1: This cartoon is adapted from xkcd. The original rollover text says: ” They say you can’t argue with results, but what kind of defeatist attitude is that? If you stick with it, you can argue with ANYTHING.”. See this link for a more detailed explanation.

Links to: Summary. Chatbot tutor. Questions. Glossary. R functions. More resources.

Chapter summary

We almost never know the truth (the population parameter), but we estimate it from a sample. Random chance (aka sampling error) ensures that our estimate will deviate from the true parameter. If sampling error is our only issue we can envision the β€œsampling distribution” – a histogram of what we would see if we repeated our study many times to characterize uncertainty. We quantify uncertainty as the β€œstandard error” i.e. the standard deviation of the sampling distribution. We can decrease sampling error by increasing sample size. When samples are non-independent, we tend to underestimate our sampling error. When samples are not chosen at random, β€œsampling bias” can generate a systematic deviation between estimates and true population parameters. Random sampling is our best protection against non-independence and sampling bias.

Chatbot tutor

Please interact with this custom chatbot (link here) I have made to help you with this chapter. I suggest interacting with at least ten back-and-forths to ramp up and then stopping when you feel like you got what you needed from it.

Practice Questions

Try these questions! By using the R environment you can work without leaving this β€œbook”. To help you jump right into thinking and analysis.

Q1) The ___ describes the variability among individual observations in a sample (or population). In other words, the ____ quantifies how far we expect individuals to deviate from the sample estimate. .

Q2) The ___ describes the variability among estimates (of a fixed size) from a population. In other words, the ____ quantifies how far we expect sample estimates to deviate from the population parameter. .

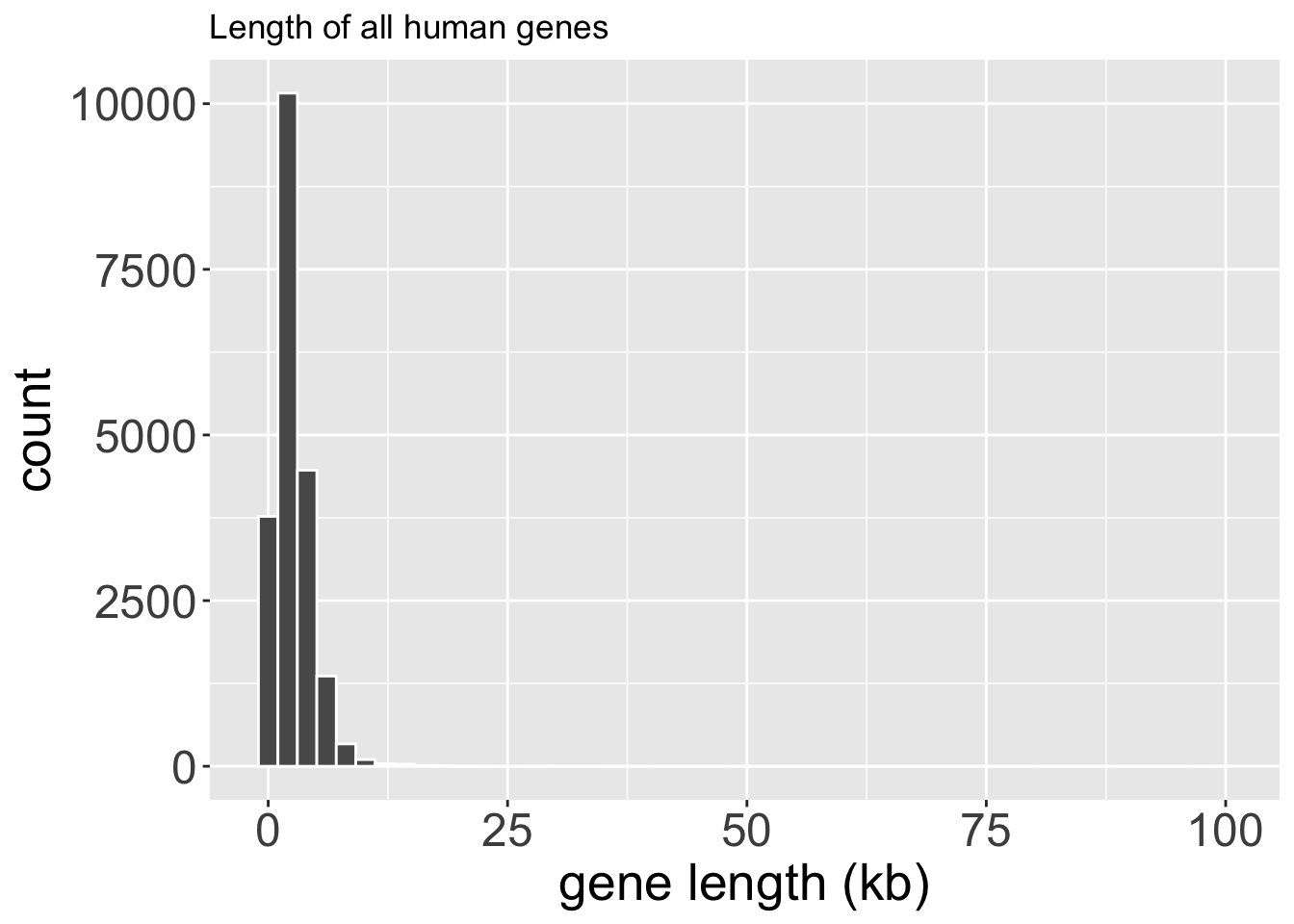
A histogram showing the distribution of lengths for all human genes. The figure shouws that the most human genes are relatively short (median around 3kb), with a few genes being exceptionally long.
Figure 2: A histogram showing the distribution of lengths for all human genes. Most are very small, the median is less than 3kb!
Q3) As seen in Figure 2, the distribution of human gene lengths is ___ (find all correct)

.

Q4) Figure 2 displays ___

Sampling wrong: I tried to create a sampling distribution for median human gene length by randomly selecting nucleotides from the human exome, finding the gene they were in, noting its length, and removing it from my list until I had the lengths of fifty genes in the human genome. I did this one thousand times to get medians from one thousand samples of size fifty (Figure 3).

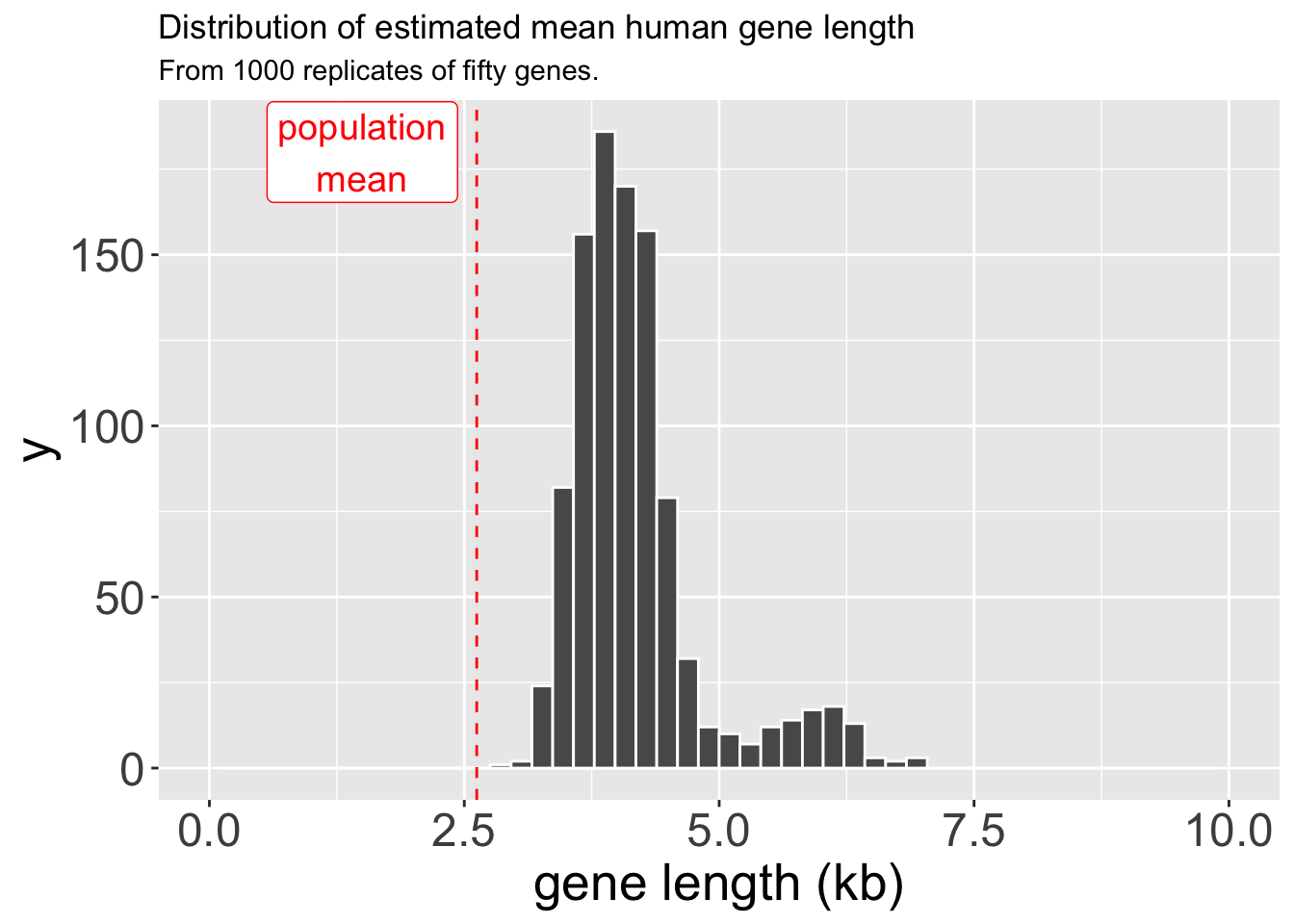
The distribution of estimated mean human gene length from 1000 replicates of fifty genes. The x-axis is gene length (kb) from 0 to 10. The data is concentrated between 3 and 6 kb, with the tallest peak centered around 4 kb, and a second smaller peak near 5.5 kb. A vertical dashed red line showing the actual population mean is shown at approximately 2.8 kb, to the left of the main cluster of data.
Figure 3: The distribution of the estimated mean length of human genes. Here is how I sampled to get this distribution: (1) A base pair is randomly selected from the human genome. (2) If it falls within a gene, that gene’s length is recorded. If not, another base pair is chosen at random. (3) This process continues until 50 genes have been sampled.
Q5) The difference between the true population mean (red line) and my estimates from samples of size fifty (bars in histogram) are most likely explained by

.

Q6) YANIV INSERT CHATBOT. Explain your reasoning for the answer above. Any guesses on how I could have gotten this so wrong? How could this be fixed?

Q7) Why is the range of values so much smaller in Figure 3 than in Figure 2?

For the following questions, refer to Figure 4 (right).

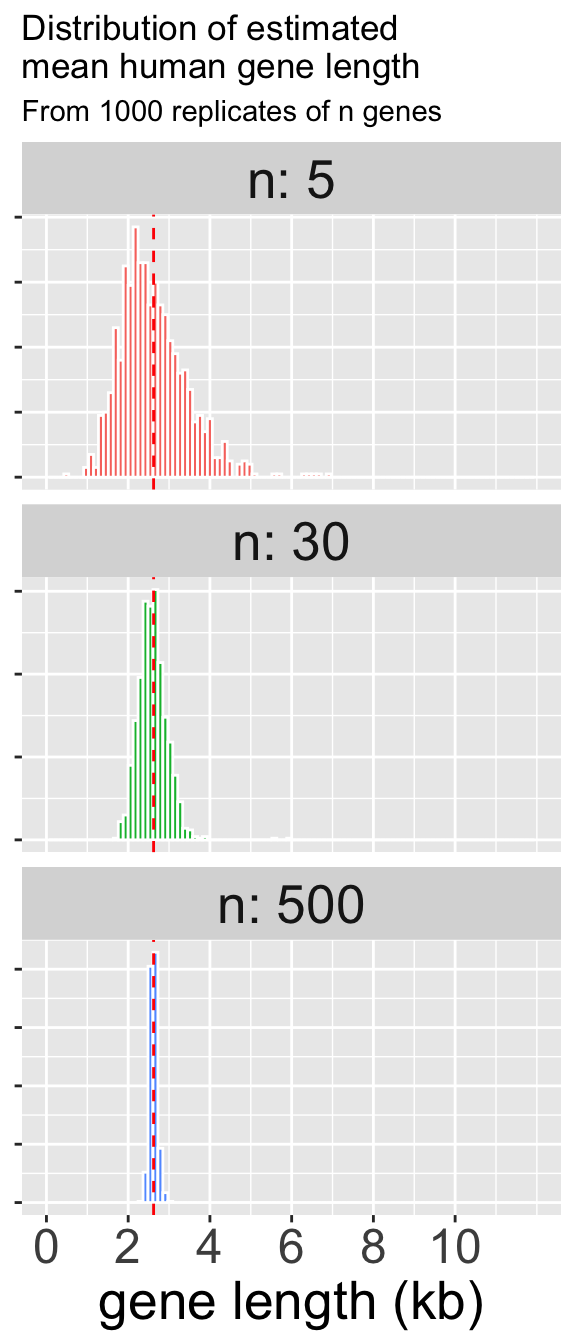
A multi-panel plot showing three histograms of estimated mean human gene length, illustrating the effect of sample size. The panels are stacked vertically for sample sizes of n=5, n=30, and n=500. As the sample size increases down the chart, the histogram becomes dramatically narrower, indicating that the estimates of the mean are much less variable and more precise. The top plot (n=5) is wide and red, the middle (n=30) is narrower and green, and the bottom (n=500) is extremely narrow and blue. A vertical dashed red line in each plot marks the mean of the estimates.
Figure 4: The effect of sample size on the sampling distribution of the mean human gene length. Each panel shows a histogram of 1,000 sample means, with each mean calculated from a random sample of n genes.
Q8) What aspect of sampling is responsible for the difference between the plots in Figure 4?
Q9) Which sample size is associated with the smallest standard error?

Q10) For the sampling distribution for samples of size n in Figure 4, approximately what proportion samples have a mean greater than the population mean?

  • n = 5: .
  • n = 500: .

Q11) For the sampling distribution for samples of size n in Figure 4, approximately what proportion samples have a mean greater than 3.8 kb?

  • n = 30: .
  • n = 500: .

REFRESHER For the questions below summarize the gene lengths data set. If there is not an answer, type NA.

Q12) The mean gene length is .

Q13) The standard deviation in gene length .

Q14) The standard error in estimated gene length .

πŸ“Š Glossary of Terms

Convenience sampling (aka haphazard sampling): Sampling whatever is easiest or closest.

Independent sample A sample where knowing something about one observation tells you nothing about the others.

Non-independent sample A sample where some observations are related to each other. This messes with your uncertainty estimates unless accounted for.

Parameter: A number that describes the truth about a population (e.g. the actual mean petal area of all Clarkia xantiana plants on Earth).

Pseudoreplication: Using repeated but non-independent measurements as if they were independent. This can lead to overconfidence and misleading results.

Random sample: A sample where each individual has an equal chance of being selected.

Sampling: Selecting a subset of individuals from a population.

Sampling Bias: Any process that causes a sample to be systematically unrepresentative of the population.

Sampling Distribution: A histogram of what you’d get if you repeated your study over and over, taking a new sample each time and recording the resulting estimate.

Sampling Error: The random difference between an estimate from a sample and the true population parameter.

Standard Error (SE): The standard deviation of the sampling distribution. Measures the expected variability in your estimates due to sampling error.

Survivorship bias: A kind of sampling bias where you only observe individuals that survive some process (e.g., returning warplanes), which can give a misleading picture of the whole population.

Key R Functions

Additional resources

Readings: